作者:郭sy 时间:2025-07-08
斯奈尔定律(又称折射定律)描述了光在两种不同介质界面发生折射时,入射角与折射角之间的关系,是几何光学的基本定律之一。当光从介质1(折射率n1)斜射入介质2(折射率n2)时。满足以下光学关系式。
n1sinθ1=n2sinθ2
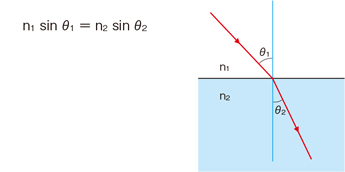
斯奈尔定律,其中θ1是入射角,θ2是折射角。n1和n2是两种介质的绝对折射率。
反射率(垂直入射)R0当光垂直入射(入射角𝜃=0°)到两种介质的界面时,反射率的计算简化为仅与介质的折射率相关,无需考虑角度。其光学关系式如下:
R0=【(n1-n2)/(n1+n2 )】2
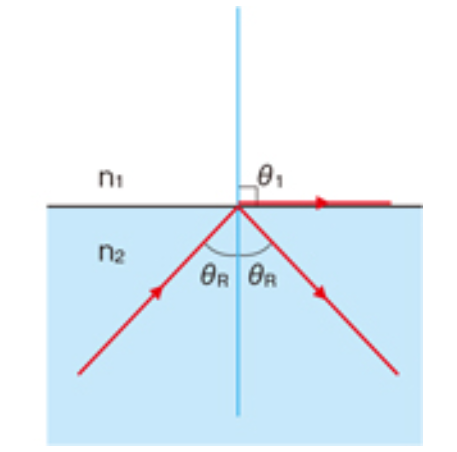
临界角θR=θ2,临界角是光从光密介质(折射率𝑛1)射向光疏介质(折射率n2,且𝑛1>𝑛2)时,发生全反射(Total Internal Reflection, TIR)的最小入射角。当入射角≥临界角时,光不再折射,而是全部反射回原介质。
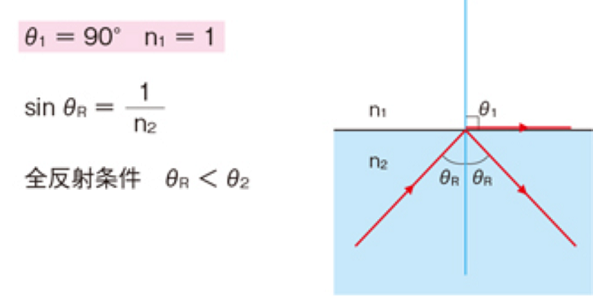
θ1=90°,n1=1
sinθR=1/n2
全反射条件:1光密介质到光疏介质;2入射角大于临界角 θ2>θR
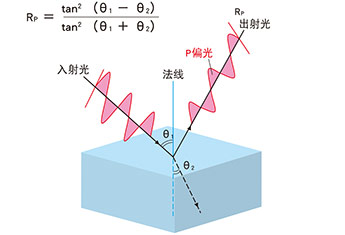
反射率(P偏光)RP,P偏光(平行偏振光) 的反射率 Rp表示光在界面反射时,电场矢量平行于入射面的光能反射比例。与S偏光不同,P偏光在特定角度(布儒斯特角)下反射率可降为0。几何光学如下。
Rp=tan2(θ1-θ2 )/tan2 (θ1+θ2 )
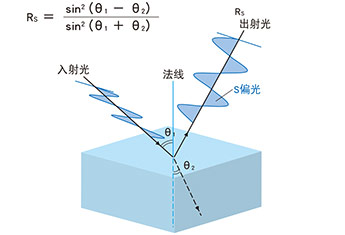
反射率(S偏光)Rs,是指 S偏振光(TE偏振光,电场方向垂直于入射面)在介质表面反射时,反射光功率与入射光功率的比值。其计算公式基于菲涅尔反射定律,具体如下。
Rs=sin2 (θ1-θ2 )/sin2 (θ1+θ2 )
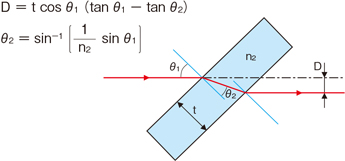
平行平板的光束移动D,)是指光线穿过平板后,出射光线相对于入射光线在 横向方向(平行于平板表面) 上的平移距离。这一现象是由于光线在平板的两个界面(入射面和出射面)发生折射导致的。
D=tcosθ1 (tanθ1-tanθ2 )
θ2=sin-1 |1/n2sinθ1 |
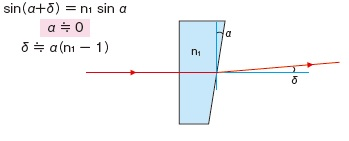
楔形板的光束偏向角δ,楔形板(Wedge Plate)是由两个不平行的平面构成的透明光学元件(如玻璃楔镜),其特点是两表面之间存在一个小的夹角α(楔角)。当光线通过楔形板时,由于折射作用,出射光线相对于入射光线会发生偏向,其角度变化称为偏向角δ。
sin (α+δ)=n1sinα
α→0
δ→α(n1-1)
光学密度OD,是衡量材料对光吸收能力或衰减程度的对数尺度参数,广泛应用于光学、光谱学、激光防护、摄影和生物医学等领域。
OD=log(I1/I2 )=-log(T)
T:透过率,I1:入射光强,I2:出射光强
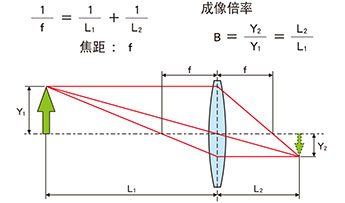
透镜是光学系统中的核心元件,用于聚焦或发散光线。透镜的公式如下。
1/f=1/L1 +1/L2
B=Y2/Y1 =L2/L1
透镜的合成焦距,当多个透镜组合在一起时(如紧密接触或有一定间隔),其整体光学效果可以用一个等效透镜 来描述,该等效透镜的焦距称为合成焦距。计算合成焦距的公式:
fs=(f1f2)/(f1+f2-d)
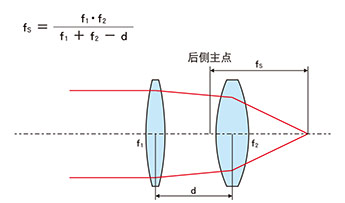
单透镜的焦距
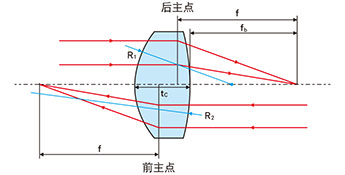
厚透镜的焦距
双凸透镜条件: R1>0,R2<0
1/f=(n-1){1/R1 -1/R2 +tc (n-1)/(R1R2n)}
fb=f{1-tc (n-1)/(nR1 )}
双凸透镜的焦距
双凸对称透镜的条件:R1=-R2=R
f=nR2/(n-1){2nR-tc(n-1)}
fb=f{1-tc(n-1)/nR}
球形透镜的焦距
球形透镜条件:2R=tc
f=nR/2(n-1)
fb=f-R
平凸透镜的焦距
平凸透镜条件:R1>0,R2=∞
f=R1/(n-1)
fb=f-tc/n
光束扩束器(Beam Expander)是一种光学系统,用于增大或缩小激光光束的直径,同时调整其发散角。光束扩束器的倍率B如下。
伽利略式
B=fp/fN =C2/C1
开普勒式
B=f2/f1 =C2/C1

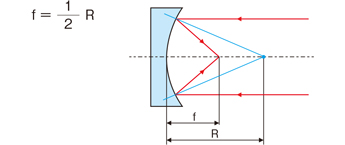
凹面镜的焦点,凹面镜(Concave Mirror)是一种反射镜,其反射面为球面或抛物面的一部分,能够会聚光线形成实像或虚像。其焦点(Focal Point)是平行于主光轴的光线反射后会聚的点,计算公式如下:
f=1/2*R
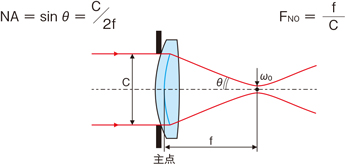
激光聚光公式。激光聚光(聚焦)是指利用透镜或反射镜将激光束会聚到最小光斑(焦点)的过程。
NA=sinθ=C/2f
FNO=f/C
主要光学公式光束的束腰1/e2,在激光光学中,束腰(w0是高斯光束的最小光束半径(即光束最窄处的半径),通常定义为光强下降到峰值强度的1/e2(约 13.5%)时的横向距离。束腰是描述激光光束传播特性的核心参数之一。
ω0=λ/(π×NA)
主要光学公式显微镜分辨率。显微镜的分辨率(Resolution)是指其能够清晰区分两个相邻物点的最小距离,通常由阿贝衍射极限(Abbe Diffraction Limit)决定。核心公式如下。
δ=0.61λ/NA