作者:沈wg 时间:2026-01-15
本文系统讲解偏振光学中的核心理论与工具,深入解析庞加莱球(又称邦加球)的几何模型及其与斯托克斯参量的对应关系,阐明如何将任意偏振态(线偏振、圆偏振、椭圆偏振)唯一映射到球面上的点。文章进一步结合四分之一波片和半波片的作用和庞加莱球的实际物理意义,展示偏振态在庞加莱球上的演化路径,并以此为基础介绍偏振器件的作用可视化。
偏振光的表示方式有很多种,包括:琼斯矢量:适用于完全偏振光;斯托克斯参量:可描述完全、部分和非偏振光;偏振椭圆:直观展示电场矢量轨迹;庞加莱球:基于斯托克斯参量的几何表示。
庞加莱球之所以流行,是因为它把复杂的偏振物理“翻译”成了直观的几何语言——既保留了数学严谨性,又具备工程实用性,还能扩展到前沿光场调控领域。空间三轴分别代表光路调节中最常用的水平/垂直偏振、45°偏振和左旋右旋偏振,不仅在数学转换和空间对应上逻辑严密,而且方便地适配实际光路调节中的各种常见偏振态。
1. 庞加莱球的核心优势
(1)几何直观性
庞加莱球将抽象的偏振态映射到一个三维球面上,使得各种偏振态(线偏振、圆偏振、椭圆偏振)及其关系一目了然:
赤道 → 所有线偏振态(方位角从 0° 到 180°);
北极/南极 → 右旋/左旋圆偏振;
其他点 → 各种椭圆偏振(上半球右旋,下半球左旋);
球心 → 完全非偏振光;
球内点 → 部分偏振光(偏振度< 1)。
这种“一眼看懂”的可视化能力,是代数表达(如琼斯矢量)难以比拟的。
(2)统一描述所有偏振态
琼斯矢量只能处理完全偏振光;
庞加莱球基于斯托克斯参量,天然支持完全、部分、非偏振光的统一描述;
特别适合实际光学系统中存在散射、退偏等复杂情况的分析。
(3)偏振器件的作用可视化
在光学元件(如波片、偏振片、液晶调制器)作用下,偏振态会发生变化。这些变换在庞加莱球上表现为旋转操作:
例如,一个半波片会使偏振态绕某轴旋转 180°(具体过程分析见本文最后一部分);四分之一波片引起 90° 旋转;
多个元件级联 → 多次旋转 → 可用球面几何或矩阵乘法快速计算。
这种“旋转对应变换”的特性,极大简化了偏振控制系统的设计与仿真。
(4)适用于矢量光束与高阶结构光
近年来,矢量涡旋光束(Vector vortex beams)因其空间变化的偏振分布,在光镊、超分辨成像、量子通信等领域备受关注。
传统方法难以描述其局部偏振的空间演化,而高阶庞加莱球将轨道角动量(OAM)与偏振耦合,每个点代表一种结构化偏振态,成为研究这类光束的标准工具。
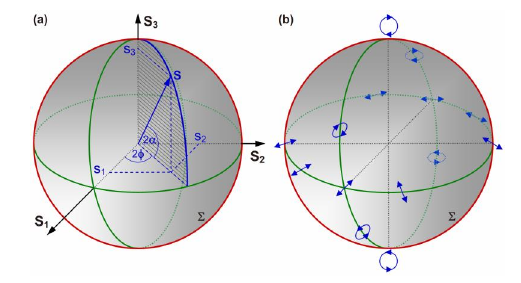
庞加莱球。(a)为庞加莱球的坐标,(b)庞加莱球表面的偏振态分布
2. 表征偏振态的斯托克斯参量法
在1852年,Stocks利用光场中可测量的参量来表示了偏振态。其中S1、S2、S3用来表示偏振态,S0表示光场强度。
S0 = E2 0x + E2 0y,
S1 = E2 0x - E2 0y,
S2 = 2E0xE0ycosδ,
S3 = 2E0xE0ysinδ
而对于两个正交的分量,可以用复数形式来表示:
Ex = E0x exp(jδx)
Ey = E0y exp(jδy)
其中δ=δy-δx,基于斯托克斯参量,我们将光场的偏振度定义为
P=(S12+S22+S32)1/2 / S0
当P=1时,即S02 = S12+S22+S32,对应的是完全偏振光;当0<P<1时,S02>S12+S22+S32,对应的是部分偏振光;当P=0时,对应的是自然光。 eq/f(1,2)
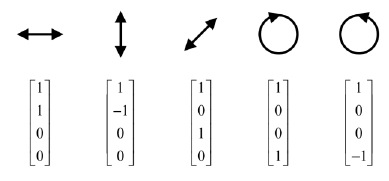
典型偏振态的斯托克斯参量
3. 庞加莱球的定义
庞加莱基于偏振椭圆的椭偏率tanα和长轴方向φ,庞加莱球将斯托克斯参量表示为:
S1=S0cos2αcos2φ
S2=S0cos2αsin2φ
S3=S0sin2α
通过这种方式将斯托克斯参量表示在一个球上,这个球被称为庞加莱球。其中球的经度为2φ,纬度为2α。
4. 庞加莱球的实际物理意义
在庞加莱球表示法中,S1、S2和S3是斯托克斯参数,它们用于描述光的偏振状态。具体来说:
S1 参数表示的是水平(H)与垂直(V)线偏振之间的差异。
S2 参数表示的是+45°和-45°线偏振之间的差异。
S3 参数则代表左旋圆偏振光(LCP)和右旋圆偏振光(RCP)之间的差异。
“S1 参数表示的是水平(H)与垂直(V)线偏振之间的差异”可以理解为:
S1 轴是在庞加莱球中的x轴,它用来量化水平偏振态(H)和垂直偏振态(V)之间的相对强度差。
当一个光束的偏振状态完全为水平偏振时,在庞加莱球上它的坐标会使得S1达到最大正值,此时S1 > 0。
相反,如果光束是完全垂直偏振,则其在庞加莱球上的坐标将使S1达到最大负值,即S1 < 0。
如果光束同时包含相等的水平和垂直分量,则 S1 = 0。这可能意味着它是某种形式的椭圆偏振光或者圆偏振光(取决于 S2 和 S3 的值)。
简而言之,S1 参数帮助我们确定光束是否更倾向于水平偏振(S1 > 0),垂直偏振(S1 < 0),或者是两者之间的某一种组合(S1 = 0)。通过这种方式,S1 轴能够清晰地表达出水平与垂直线偏振成分之间的差异。
5. 基于庞加莱球的偏振器件的作用可视化
偏振光学元件(如波片、偏振片、法拉第旋转器等)对偏振态的改变,基于庞加莱球的实际物理意义可表示为庞加莱球上的旋转操作:
半波片(HWP):绕对应快轴方向的轴旋转180°
四分之一波片(QWP):绕快轴方向旋转 90°
偏振旋转器:绕 S₃ 轴(z轴)旋转,改变线偏振方向
这种偏振器件的作用可视化视角极大简化了复杂偏振系统的设计与分析。
怎么理解“半波片(HWP):绕对应快轴方向的轴旋转180°”这句话呢?
(1)在庞加莱球上:所有线偏振态都位于赤道上。线偏振方向φ对应赤道上角度为2φ的点(注意:球面角度是偏振角的两倍,这是由斯托克斯参量定义决定的)。
(2)“绕快轴方向的轴旋转180°”的含义
--“快轴方向”在庞加莱球上对应哪个轴?
快轴是一个线偏振方向,比如快轴在角度φ。那么它在庞加莱球赤道上对应的点就是 (S₁, S₂, S₃) = (cos 2φ, sin 2φ, 0)。这个点定义了球面上的一个直径方向,也就是一个旋转轴(穿过球心和该点的直线)。
--半波片的作用 = 绕该轴旋转 180°
在庞加莱球上,任何偏振态经过半波片后,相当于将该点绕上述轴旋转 180°。这个旋转操作会把入射偏振态映射到出射偏振态。
举例说明:设半波片快轴为水平方向(φ= 0°);快轴在庞加莱球上对应点:(1, 0, 0) → 即S1轴,所以半波片的作用为绕S1轴旋转180°。当入射光为45°线偏振→庞加莱球上点为 (0, 1, 0)。绕 S1轴旋转 180° 后:y → -y,z →-z,所以 (0, 1, 0) → (0, -1, 0)。(0, -1, 0) 对应 -45°(或135°)线偏振,与实操结果一致!
再比如:
快轴为22.5° → 对应庞加莱球上方向角45°,即轴向量为(cos45°, sin45°, 0) = (√2/2, √2/2, 0)
绕此轴旋转180°,会把水平偏振(1,0,0)映射到45°偏振 (0,1,0)
四分之一波片在庞加莱球上的操作与半波片一致,只是旋转角度变为90°。
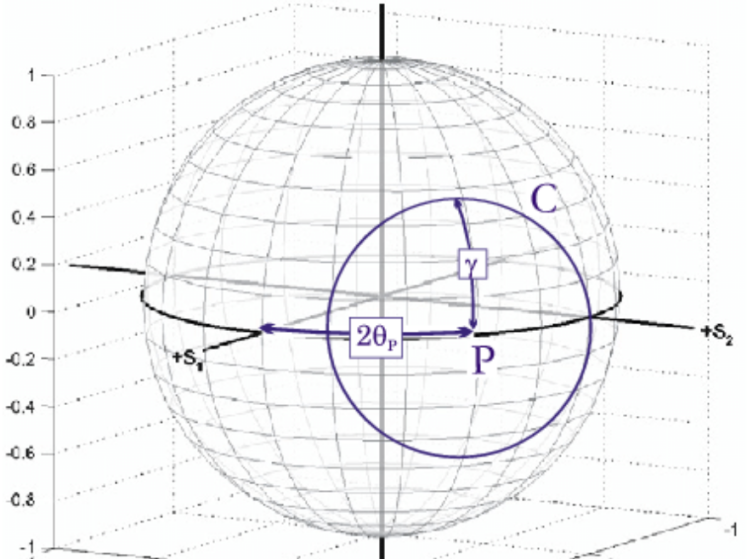
使用波片在邦加球上移动偏振光
邦加球的核心优势在于将复杂的代数计算和物理过程转化为直观的几何操作。它不仅是进行偏振态分析与控制的有力工具,更是现代光通信(PMD管理)、光学测量和量子技术等领域中不可或缺的工程设计和故障诊断手段。